A Careful Look At Projection Matrices
I’ve been writing graphics programs in vulkan more recently. I wrote most of my math code for vector and matrix operations with the OpenGL coordinate system in mind.
I find myself re-deriving these matrices every time I switch APIs to understand exactly what’s going on.
So, I decided to make a reference where I derive and spell out precisely the difference between projection transformations in OpenGL and Vulkan. I’ll include the orthographic and perspective transformations in what follows.
These functions directly mirror the derivations shown below.
Camera coordinate system
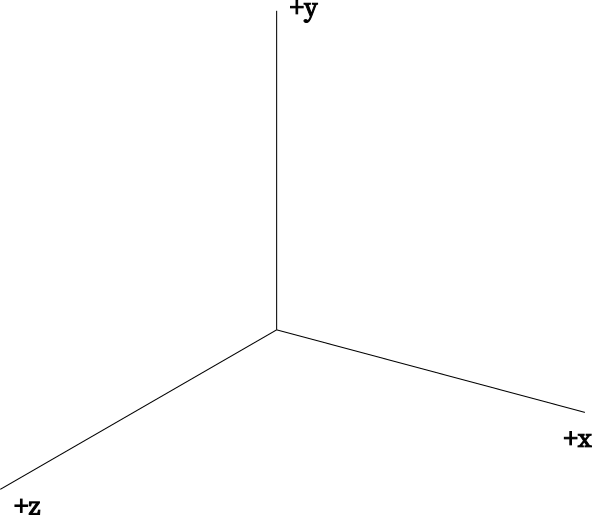
Here I’ll be assuming a camera where after the view transformation, the positive y-axis is up,the positive x-axis is right, and the positive z-axis is towards the viewer.
OpenGL coordinate system
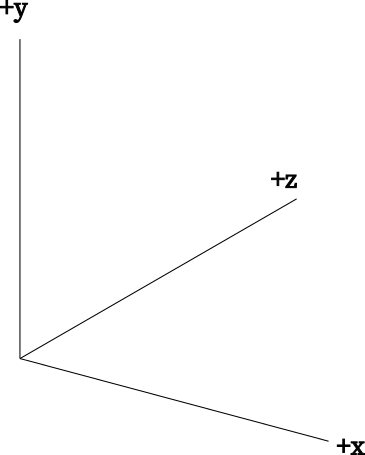
Let \(T_{GL}\) be the transformation from the camera-local space to the OpenGL clip-space.
So \(T_{GL} =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\)
Vulkan coordinate system
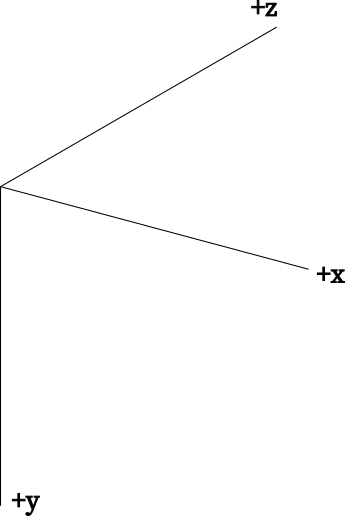
Let \(T_{VK}\) be the transformation from the camera-local space to the Vulkan clip-space.
So \(T_{VK} =\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\)
Through the following, I’m going to use \(\textbf{p} = (x,y,z,1)\) to refer to the old position (camera-local space) and \(\textbf{p}' = (x',y',z',w')\) to refer to the new position (clip-space) .
Orthographic Projection
Let’s start with OpenGL
We want to map \([l,r] \times [b,t] \times [n,f] \to [-1,1]^3\).
This does the job: \(x' = 2(\frac{x - l}{r - l}) - 1 = (\frac{2}{r-l})x - (\frac{r+l}{r-l})\). The y-axis and z-axis are derived in the same way.
The orthographic projection matrix is \(P_{ortho,GL} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{f - n} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix} * T_{GL} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{f - n} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{-2}{f - n} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
Now, Vulkan
We want to map \([l,r] \times [b,t] \times [n,f] \to [-1,1] \times [1,-1] \times [0,1]\).
The x-axis is the same as in OpenGL. The y-axis is swapped, so \(y' = -2(\frac{y - b}{t - b}) + 1 = (\frac{-2}{t-b})y + (\frac{t+b}{t-b})\).
As for the z-axis, we get \(z' = \frac{z - n}{f - n} = \frac{z}{f - n} - \frac{n}{f - n}\)
Putting this into a matrix gives \(P_{ortho,VK} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{b - t} & 0 & -\frac{t+b}{b-t} \\ 0 & 0 & \frac{1}{f - n} & -\frac{n}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix} * T_{VK} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{b - t} & 0 & -\frac{t+b}{b-t} \\ 0 & 0 & \frac{1}{f - n} & -\frac{n}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & -\frac{2}{b - t} & 0 & -\frac{t+b}{b-t} \\ 0 & 0 & -\frac{1}{f - n} & -\frac{n}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix}\)
Perspective projection
The perspective matrix is applied before a orthographic projection matrix. Normally, people just combine these two matrices into one.
Separating the perspective matrix out as first is useful (at least conceptually), because it’s the same between OpenGL and Vulkan.
We want to map the viewing frustrum to a cube with extents \([l,r] \times [b,t] \times [n,f]\)
In each case we have \(x' = \frac{n x}{z}, y' = \frac{n y}{z}\). This division by \(z\) is a bit of problem since we can’t represent that in a matrix transformation.
But both OpenGL and Vulkan perform the perspective-divide \((x',y',z',w') \to (\frac{x'}{w'},\frac{y'}{w'},\frac{z'}{w'})\) after the transformations have been applied so the division can happen automatically for us.
We can instead update \(x' = nx,y' = nx\), pretty simple.
As for \(z'\), we would keep \(z' = z\), since we want to store depth information. But we know the perspective-divide is ultimately going to happen after our transformation.
The question then is, for what constants \(a,b\) can we have: \(\frac{az + b}{z} = z\) or \(az + b = z^2\).
Applying the near and far plane constraints gives \(an + b = n^2\) and \(af + b = f^2\). Solving gives \(a = n + f,b = -nf\).
Finally, sticking this all into a matrix we get \(P_{persp} =\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0\\ \end{bmatrix}\)
For OpenGL
we have the following final perspective projection matrix \(P_{persp,GL} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{f - n} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix} * \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0\\ \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ = \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t - b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{n+f}{f -n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0\\ \end{bmatrix}\)
And for Vulkan
\[P_{persp,VK} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{b - t} & 0 & -\frac{t+b}{b-t} \\ 0 & 0 & \frac{1}{f - n} & -\frac{n}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix} * \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0\\ \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \\ = \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & -\frac{2n}{b - t} & \frac{t+b}{b-t} & 0 \\ 0 & 0 & -\frac{f}{f -n} & -\frac{nf}{f-n} \\ 0 & 0 & -1 & 0\\ \end{bmatrix}\]Summary
The OpenGL projection matrices are:
\[P_{ortho,GL} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t - b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{-2}{f - n} & -\frac{n+f}{f-n} \\ 0 & 0 & 0 & 1 \end{bmatrix}\] \[P_{persp,GL} = \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t - b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{n+f}{f -n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0\\ \end{bmatrix}\]The Vulkan projection matrices are:
\[P_{ortho,VK} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & -\frac{2}{b - t} & 0 & -\frac{t+b}{b-t} \\ 0 & 0 & -\frac{1}{f - n} & -\frac{n}{f-n} \\ 0 & 0 & 0 & 1\\ \end{bmatrix}\] \[P_{persp,VK} = \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & -\frac{2n}{b - t} & \frac{t+b}{b-t} & 0 \\ 0 & 0 & -\frac{f}{f -n} & -\frac{nf}{f-n} \\ 0 & 0 & -1 & 0\\ \end{bmatrix}\]